이 포스트는 Coursera Machine Learning 강의(Andrew Ng 교수)를 요약 정리한 것 입니다. 포스트에 사용된 이미지 중 많은 내용은 동영상 강의 자료의 이미지 캡쳐임을 밝힙니다.
Course Home: Coursera Machine Learning
1. Model representation
주택 가격 예측모델을 다시 한번 살펴보자. 집의 크기에 따라 가격이 결정(Target Value가 있고)되고, 가격은 연속형 데이터이므로 주택가격 예측모델은 지도학습(supervised Learning) 중 regression problem에 해당된다.

크기가 1250 feet2인 집을 구하려면 돈이 얼마나 필요할까? 위와 같이 straight function을 그렸다고 가정했을 때 $220K가 필요하다. 그러나 이것이 정확한 straight function은 아니다. 따라서 정확한 function을 구하기 위한 방법이 필요하게 되었다.
Straight function을 유도하기 위한 방법을 알아보자.

우선은 위와 같이 점들을 표로 나열해보자. X에 매핑되는 y값이 47개 정도 있다고 했을 때, 이 점들은 training examples이라고 하고 training examples의 수를 m 이라고 한다. X축 값은 입력변수(feature, 여기서는 집의 크기), y축 값은 결과변수(여기서는 집의 가격)이고, X(n) 은 X의 n번째 인덱스라고 정의하자. 그러면 x(1) = 2104, x(2) = 1416 이 되고, Y(1) = 460이다.
이 Training 집합을 가지고 Learning Algorithm을 통해 h(hypothesis)라는 학습된 가정을 만들어 집의 크기 X가 들어왔을 때 추정하는 y값 즉 Price($)를 구할 수 있게 된다.
Hypothesis(추론)은 추론 알고리즘의 집합으로 Hypothesis h는 Feature 넣으면 Target Value를 계산해주는 수식이다. 실제 아파트 크기(X)값을 넣으면 예측되는 가격(Y)를 도출해주는 개념인데, 이 hypothesis는 말 그대로 추론 값이므로 실제 정확한 값이라고 말할 수는 없다. 다만 예측의 정확도를 높이는 것이 중요한데, training set을 learning algorithm을 이용하여 지속적으로 학습함으로써 최적의 h를 찾는 것이 바로 머신러닝이다.

“h”는 어떻게 표현할까? 예전에 배웠던 일차함수 공식(y = ax + b)을 떠올리고 그대로 바꾸어 표현해보면 h(x) = θ0 + θ1x 이다.
2. Cost Function
아이디어는 다음과 같다. 우리가 가지고 있는 training 집합들의 모든 점들에서부터 straight function과의 거리가 가장 작은 θ0, θ1을 구하고자 하는 것이다. 이를 구하는 함수를 “cost function”이라고 한다. n은 training 집합의 개수이고 모든 점부터 y까지의 거리를 더한 후 평균으로 나누는 것이 아래 식이다.

우리의 목표는 Cost Function J(θ0,θ1) 값을 최소로 하는 θ0, θ1 을 구하는 것이다. Cost function값이 작을수록 x값이 주어졌을 때 hθ(X)의 값이 y와 근접해 진다.
직관적으로 쉽게 생각해보기 위해서 θ0의 값을 0으로 놓아 보자. 그러면 그래프는 y=ax가 되므로 hθ(x(i)) 의 값은 θ1(x) 가 된다. 따라서 hθ(x) 는 θ1에 의해서만 영향을 받게 된다. 우리의 목적은 J(θ1) 값을 최소화하는 θ1만 구하면 된다.

예를 들어 θ1 = 1인 경우 J(θ1) 값은 어떻게 될까?
θ1 =1 이기 때문에 hθ(x) = x 가 되게 되고 해당 점은 (1,1), (2,2), (3,3)에 3개가 있다. 위에 있는 식을 이용하 J(θ1)의 값을 구해보면 아래와 같다.

즉, θ1=1 일 경우 J(θ1) = 0이다.

이번에는 θ1=0.5 인 경우를 대입해보자.


이제 모든 θ1 에 대한 J(θ1) 값을 그래프로 그려보면 아래와 같이 U자 모양의 그래프가 된다.

이 때 J(θ1)를 최소로 하는 θ1 값은 1로써 이 때 J(θ1)은 0이 된다. 왼쪽 그림처럼 h값과 실제 y값이 정확히 같기 때문에 J는 0이 되다.
그러면 다시 주택 가격 예측 문제를 생각해보자.

위의 straight function 은 θ0=50, θ1=0.06 일 때의 그래프이다. 이 straight function은 실제 값(y)에서 많이 떨어져 있기 때문에 이상적인 값은 아니다. 이때 J(θ0, θ1)의 그래프는 어떻게 그려질까? θ1만 있을 때와 비슷한 모양이긴 하나, 아래와 같이 3차원 평면이 된다.

아래 그림은 J(θ0, θ1) 의 contour plots (등고선 선도)이다. 같은 색깔의 점은 모두 같은 J(θ0, θ1) 의 값을 가지게 된다. θ0, θ1 값이 다르더라도 X1, X2의 J(θ0, θ1) 값은 같다.

training data에 대한 h값과 실제 관측값의 차이가 적을수록 J가 적어지므로 아래 current hypothesis가 정확해 질수록 등고선 안쪽으로 가까워 지는 것을 볼 수 있다.

아래의 그림에서 hypothesis는 J(θ0, θ1)의 contour plots 가장 안쪽으로 들어왔기 때문에 거의 이상적인 함수라 볼 수 있다.

그래서 우리는 이 J값을 줄이기 위해 머신 러닝을 적용하고자 한다.
- 특정한 θ0, θ1 값을 정한다.
- θ0, θ1 값을 바꾸면서 J(θ0, θ1)값이 최소가 될 때까지 진행한다.
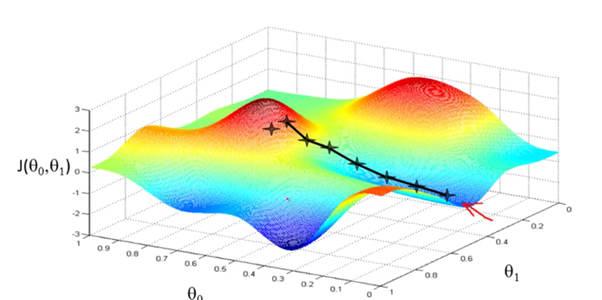
우리는 높은 산에서 가장 낮은 저지대로 간다고 생각해보자.
- 우선은 가장 높은 점의 대략 어느 부분을 선택한다.
- 그리고 빠르게 내려가기 위해서 주변을 살피고 나서 가장 가파른 곳을 선택하여 내려간다.
- 그 다음 또 주변을 살피고 어느 곳이 가장 가파르게 내려가는지를 계산하여 길을 선택한다.
- 그렇게 계속 하다보면 가장 최소값을 가지는 J(θ0, θ1)값을 선택하게 되고 더 이상 내려가지 않게 된다.

물론 처음 시작을 다른 지점에서 시작한다면 다른 결과를 얻을 수도 있다.

이러한 계산 알고리즘을 Gradient descent algorithm 이라고 한다.
(Coursera ML class – week01 Linear regression with one Variable part II로 이어집니다.)
Course Home: Coursera Machine Learning
Andrew Ng 교수님 소개: https://www.coursera.org/instructor/andrewng
2 thoughts on “Coursera ML class – week01 Linear regression with one Variable part I”